常用查找算法

查找算法

本文为数据结构与算法之美-王争的学习笔记，如需查看完整内容，请参考链接。

二分查找（Binary Search）

原理

假设有1000万个整数数据，每个数据占8个字节。如何设计数据结构和算法，快速判断某个整数是否出现在这1000万个数据中？要求不能占用太多的内存空间，最多不超过100MB。

现在，假设有十条订单数据，订单金额已经从小到大进行排序，从其中找到金额为19元的订单。使用二分思想进行查找的思路如下：

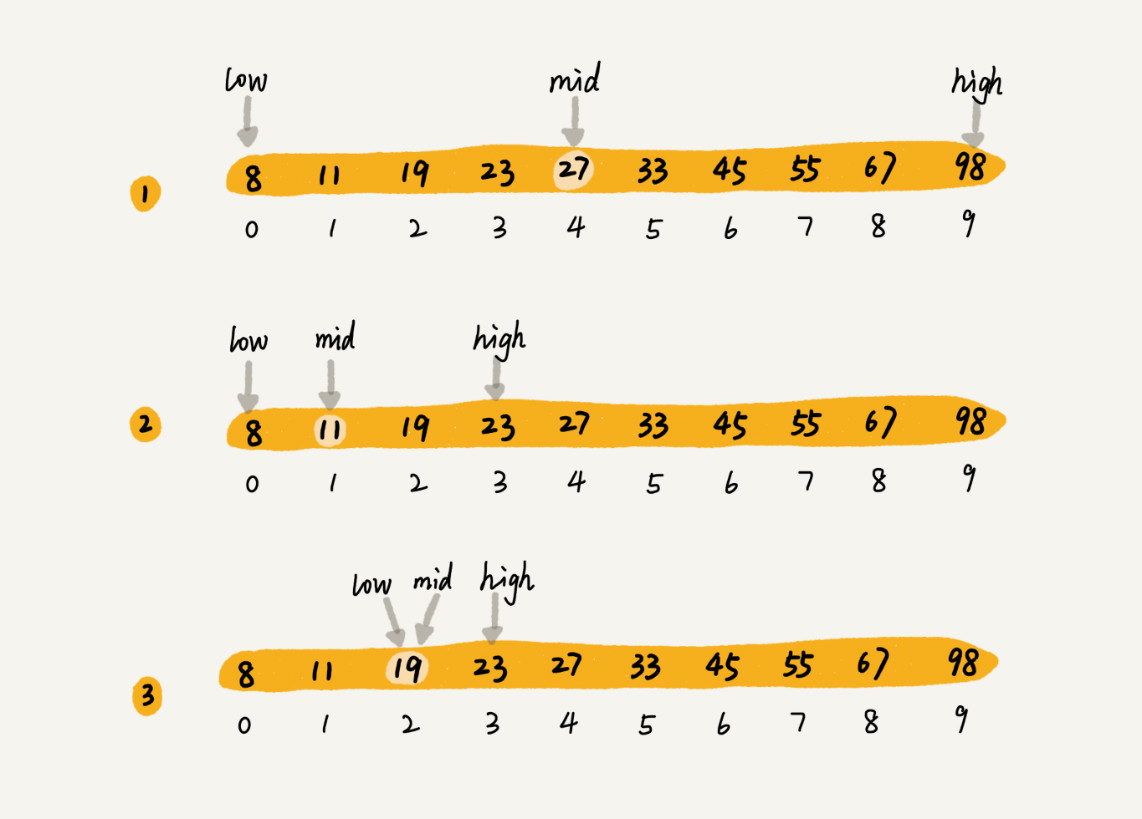
对上述的查找思想进行总结：

二分查找的对象是一个有序的数据集合，类似于分治思想。每次都跟区间的中间元素对比，将待查找的区间分半，直到找到要查找的元素，或者区间被缩小为零，则停止。

时间复杂度

假设数据大小为$n$，每次查找数据都会缩小一半。最坏情况下，当查找区间被缩小为空时，查找停止。

令$\frac{n}{2^k}=1$，求得$k=logn$，也就是说整个查找过程最多执行$logn$次，在每次查找中，只会执行简单的数据大小比较操作，因而时间复杂度为$O(logn)$。

$O(logn)$被称作对数时间复杂度，这是一种非常高效的时间复杂度，在一定情况下比常量级$O(1)$时间复杂度还高效。

在使用大$O$标记法表示时间复杂度时，会忽略掉常数、系数和低阶，当常量的值很大时，例如$O(1000)$等，常量级的时间复杂度可能就没有$O(logn)$的算法效率高。

二分查找的简单实现

假设待查找的数据中不存在重复的数据，最简单的二分查找代码如下：

循环实现

int binary_search(vector<int> array, int number) {
    // 找到则返回对应的下标，否则返回-1
    int mid = array.size() / 2;
    int begin = 0;
    int end = array.size() - 1;
    while (begin < end){
        if (array[mid] != number) {
            if (array[mid] < number)
                begin = mid + 1;
            else
                end = mid - 1;
        }
        else
            return mid;
        mid = (end - begin) / 2 + begin;
    }
    if (array[begin] == number)
        return begin;
    else
        return -1;
}

编写上述代码时，要注意while()循环的退出条件和最后的两个retrun语句的搭配，当循环退出时，还剩余一个元素未判断，因而要对该元素进行判断。

要注意的另一点是mid的更新公式，使用mid = (end - begin) / 2 + begin而不是mid = (end + begin) / 2的原因是end和begin的数值可能比较大，相加会导致数值移除。

同时还要注意begin和end的更新方式，每一更新都要将mid位置剔除在下一个查找区间之外。

递归实现

// 二分查找的递归实现
int binary_search_recursion(vector<int> array, int number){
    int begin = 0;
    int end = array.size() - 1;
    int index = binary_search_inter(array, begin, end, number);
    return index;
}


int binary_search_inter(vector<int> array, int begin, int end, int number){
    int index;
    if (begin == end)
        if (array[begin] != number) {
            return -1;
        }
        else {
            return begin;
        }

    int mid = (end - begin) / 2 + begin;
    if (array[mid] == number)
        return mid;
    else if (array[mid] > number)
        index = binary_search_inter(array, begin, mid - 1, number);
    else
        index = binary_search_inter(array, mid + 1, end, number);
    return index;
}

二分查找的应用场景

• 二分查找依赖顺序表结构，不适用于链表等链式存储结构，因为需要使用下标随机访问数组元素，顺序表的随机访问时间复杂度为$O(1)$，而链表的随机访问时间复杂度为$O(n)$。
• 二分查找适用于有序数据，数据无序则首先需要排序。排序的时间复杂度最低为$O(nlogn)$，如果数据没有频繁的插入和删除，就只需要进行一次排序；如果数据需要频繁地插入或者删除，则需要反复进行排序。因而，二分查找适用于一次排序，多次查找的场景，适合静态数据。
• 二分查找不适用于数据量较少的情况，数据量较少时直接遍历即可。但如果数据之间的比较操作比较耗时时，推荐使用二分查找，以减少比较次数。
• 数据量太大也不适合二分查找，数据量过大时，需要一整片连续的存储空间进行存储，有时很难满足这个条件。

对于开始的在1000万个有序的，单个数据大小为8字节的数据中查找某一个特定的数的问题，就可以使用二分查找来解决，二分查找不需要额外的存储空间，因而100MB的内存大小足够。而其他使用散列表、二叉树的查找方法就需要额外的空间，内存就无法满足条件。

进阶

假设我们有12万条IP区间与归属地的对应关系，如何快速定位出一个IP地址的归属地址？

二分查找的原理虽然非常简单，但是编写完全正确的二分查找代码并不容易。在上面的内容中，将二分查找的对象限定在不存在重复元素的有序数组中，但是二分查找的变形问题就比较复杂。

四种常见的二分查找变形问题：

• 查找第一个值等于给定值的元素
• 查找最后一个值等于给定值的元素
• 查找第一个大于等于给定值的元素
• 查找最后一个小于等于给定值的元素

查找第一个值等于给定值的元素

前面的二分查找算法适用于不存在重复元素的有序数据，如果数据中存在重复元素，且此时要查找的是第一个值等于给定值的元素，前面的简单二分查找算法就不适用。例如：从下述数据中查找8第一次出现的位置。

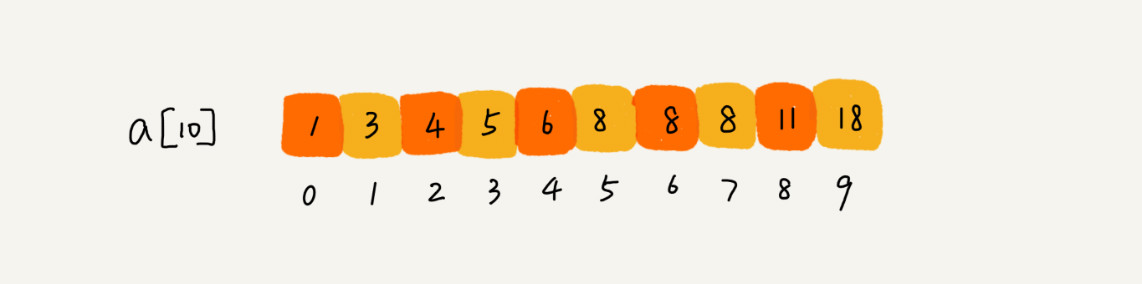
使用简单二分查找的思想，我们最终找的的数据将是a[7]位置的8，但是正确的值应该是a[5]位置的8。

思考，一个元素第一次出现的位置永远在其它出现的位置的左侧，所以当在mid位置找到目标值时，应该继续向左侧查找。一种比较难理解的写法如下：

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid = low + ((high - low) >> 1);
    if (a[mid] >= value) {
      high = mid - 1;
    } else {
      low = mid + 1;
    }
  }

  if (low < n && a[low]==value) return low;
  else return -1;
}

上述代码中，high向左侧移动的条件有两个：1. mid的值比目标值大；2. mid的值和目标值匹配，继续向左侧查找。但是这种写法不好理解。

实际上，当mid的值等于目标值时，由于数组本身是有序的，如果mid的左侧还有值，那么mid左侧紧挨着的那个元素肯定等于mid的值，否则，此时的mid即为第一次出现的位置。

下面的JAVA代码由课程作者编写：

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

下面是我自己实现的C++版本：

// 二分查找变体，从数组中查找指定元素第一次出现的位置
int binary_search_first_index(vector<int> array, int number){
    int begin = 0;
    int end = array.size() - 1;
    int mid = begin + (end - begin) / 2;
    while (begin < end || begin == end){
        if (array[mid] > number)
            // 查找左侧区间
            end = mid - 1;
        else if (array[mid] < number)
            // 查找右侧区间
            begin = mid + 1;
        else if (array[mid] == number){
            // mid为0或左侧元素不等mid处的元素时，返回mid，否则继续查找左侧区间
            if (mid == 0 || array[mid] != array[mid-1])
                return mid;
            else
                end = mid - 1;
        }
        // 注意更新中间值
        mid = begin + (end - begin) / 2;
    }
    return -1;
}

在进行工程开发时，更需要下面的代码编写方式，易读易懂才是重点。

查找等于给定元素的值中的最后一个元素的位置

与上一个问题类似，上一个问题找第一个位置，每次都需要向左侧区间查找，当前问题是查找最后一个元素，因而每次都需要向右侧区间查找。

// 二分查找变体，从数组中查找指定元素最后一次出现的位置
int binary_search_last_index(vector<int> array, int number){
    int begin = 0;
    int end = array.size() - 1;
    int mid = begin + (end - begin) / 2;
    while (begin < end || begin == end){
        if (array[mid] > number)
            // 查找左侧区间
            end = mid - 1;
        else if (array[mid] < number)
            // 查找右侧区间
            begin = mid + 1;
        else if (array[mid] == number){
            // mid为0或右侧元素不等于mid处的元素时，返回mid，否则继续查找右侧区间
            if (mid == array.size() - 1 || array[mid] != array[mid + 1])
                return mid;
            else
                begin = mid + 1;
        }
        mid = begin + (end - begin) / 2;
    }
    return -1;
}

查找第一个大于等于给定值的元素

在有序数组中，查找第一个大于等于给定值的元素。

代码实现思路和上述两种类似，下面为作者给出的Java版本的代码：

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] >= value) {
      if ((mid == 0) || (a[mid - 1] < value)) return mid;
      else high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

下面为我实现的C++版本的代码，为了明确边界判断条件，我将每一条条件语句的条件都列了出来：

int binary_search_lager_or_equal(vector<int> array, int number){
    int begin = 0;
    int end = array.size() - 1;
    int mid = begin + (end - begin) >> 1;
    while (begin < end || begin == end) {
        if (array[mid] < number) {
            begin = mid + 1;
            mid = begin + (end - begin) / 2;
        } else {
            if (array[mid - 1] > number || array[mid - 1] == number) {
                // 只有当左侧的第一个值大于number或等于number时，左侧才有可能出现大于等于number的值
                end = mid - 1;
                mid = begin + (end - begin) / 2;
            } else if (mid == 0 || array[mid - 1] < number)
                return mid;
        }
    }
    return -1;
}

查找最后一个小于等于给定值的元素

这个问题和上一个问题类似，上一个问题中，当mid处的值满足要求时，我们需要判断左侧是否可能出现满足条件的值，而在这个问题中，我们需要判断右侧是否存在满足条件的值。

作者给出的Jave版本的代码：

public int bsearch7(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

我实现的C++版本的代码：

int binary_search_smaller_or_equal(vector<int> array, int number){
    int begin = 0;
    int end = array.size() - 1;
    int mid = begin + (end - begin) >> 1;
    while (begin < end || begin == end) {
        if (array[mid] > number) {
            end = mid - 1;
        } else {
            if (mid == array.size()-1 || array[mid + 1] > number) {
                return mid;
            } else{
                begin = mid + 1;
            }
        }
        mid = begin + (end - begin) / 2;
    }
    return -1;
}

对于查找IP省份的问题，可以首先将所有IP从小到大进行排序，然后使用二分查找查找最后一个小于等于给定IP的IP。再判断当前IP是否在所查找到的IP所在的区间，如果在则返回对应的归属地，否则返回未找到。

参考

• 数据结构与算法之美