跳表
本文为数据结构与算法之美-王争的学习笔记,如需查看完整内容,请参考链接。
对于二分查找算法,其底层依赖支持随机查找特性的数组,一般情况下只能依靠数组来实现。但是,如果数据存储在链表中,是否可以实现二分查找算法呢?
为此,需要引入一种新型的动态数据结构,跳表(Skip List)。跳表可以支持快速的插入、删除和查找操作,甚至可以替代红黑树。
什么是跳表?
对于一个单链表,即使其中存储的数据是有序的,如果我们想要查找特定的值,也只能从头到尾进行遍历,时间复杂度为$O(n)$。
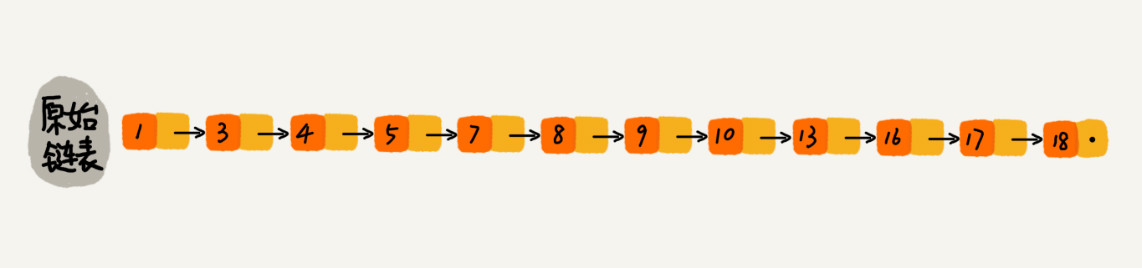
为了提高查找效率,我们可以使用额外的链表来建立查找索引,每两个结点提取一个结点到上一级,把抽取出来的一级称作索引或索引层。索引层中的每一个结点有一个down指针,该指针指向其下一级结点。
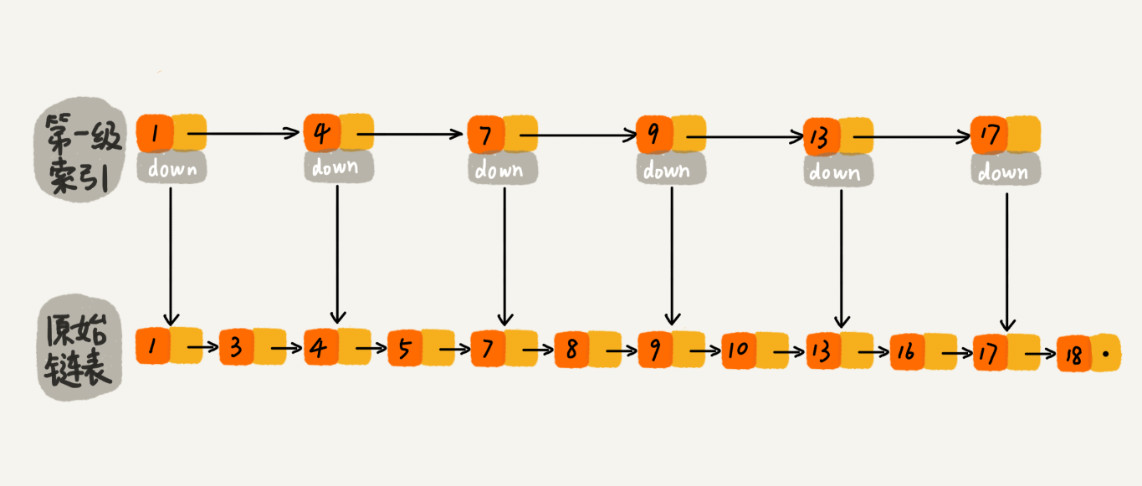
这样,如果我们要查找特定的值,例如16,便可以首先对第一级索引层进行遍历,当查找到值为13的结点时,发现其下一个结点的值为17,因为数据是有序存储的,那么16肯定在这两个结点之间。此时,只需要通过13结点的down指针转移到原始链表的13结点处,再对原始链表的13到17结点之间的元素进行查找即可很快找到值为16的结点。
在上述查找过程中,利用第一级索引层,从原先需要遍历10个结点降低为只需要遍历7个结点,跳过了中间的多个结点,查找效率大幅度提高。
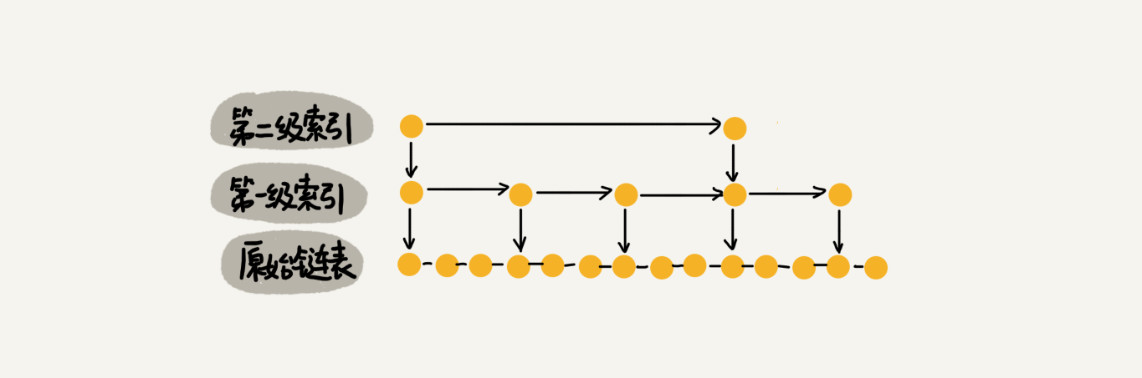
在第一级索引的基础上,还可以继续增加第二级索引,对于第一级索引中的值,每两个结点创建一个结点,如下图所示。
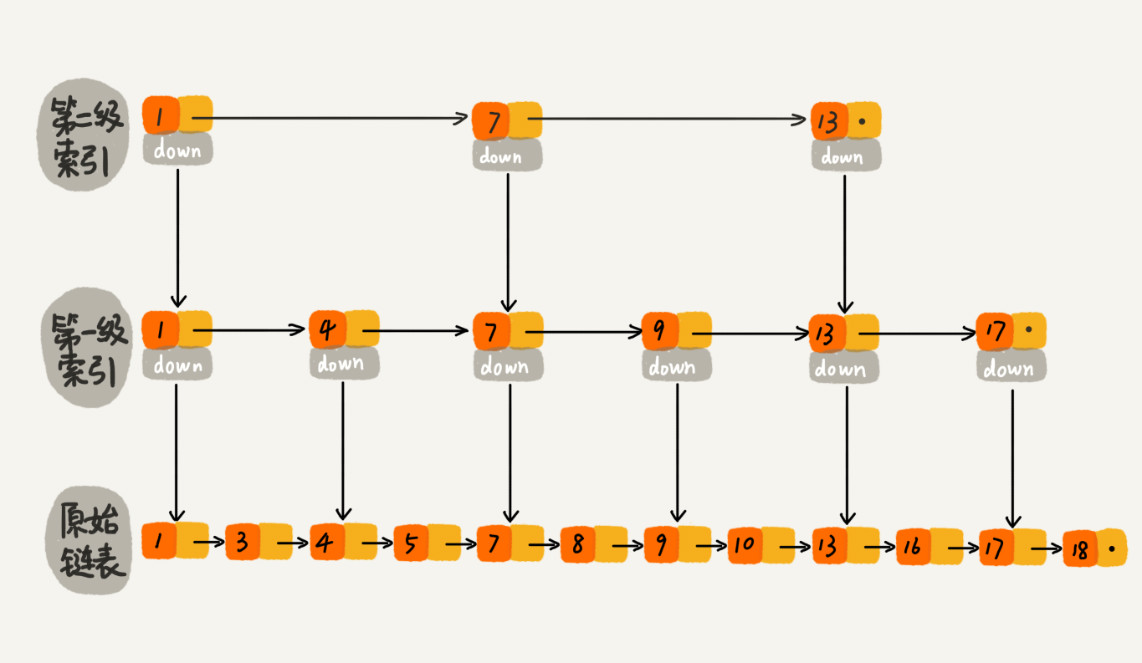
这样,如果要查找值为16的结点,就只需要遍历6个结点。
在上述例子中,由于原始结点数目不多,查找效率的提升不明显。但是,当原始结点的数目很大时,查找效率就会得到明显提升。
使用跳表进行查询的效率
在单链表中查询某个数据的时间复杂度为$O(n)$。那么,跳表的查询时间复杂度是多少?
假设链表中有n个结点,按照每两个结点抽取一个结点作为上一级索引的结点,那么第一级索引有$n/2$个结点,第二级索引有$n/4$个结点,即:第k级索引的结点个数是第k-1级索引的结点个数的$1/2$,第k级索引结点的个数为$n/(2^k)$。
假设索引有$h$级,最高级的索引有两个结点,那么$n/(2^h)=2$,求得$h=log_2n-1$,加上原始链表,整个跳表的高度为$log_2n$。假设,在跳表中查询某个数据时,每一层都需要遍历$m$个结点,那么在跳表中查询一个数据的时间复杂度为$O(m*logn)$。
如果使用上述的跳表结构,那么在每一级遍历时,最多只需要遍历3个结点。原因在于,当我们从当前级跳转到下一级索引时,当前级的两个结点之间最多只存在3个结点,那么每级最多也只需要遍历3个结点。
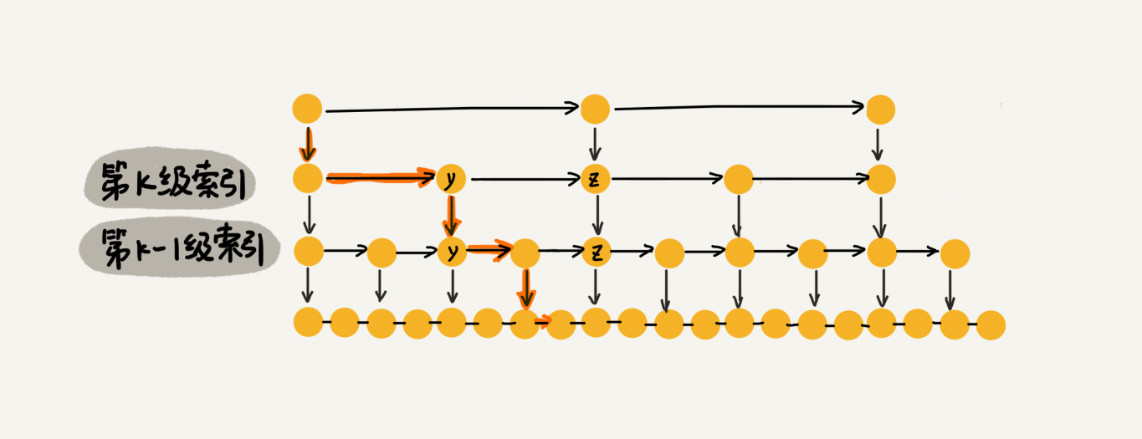
因此,在跳表中查询任意数据的时间复杂度就是$O(logn)$。查找的时间复杂度和二分查找相同。
跳表的空间复杂度
跳表的空间复杂度如下所示:

上述等比数列的和为n-2,那么空间复杂度为$O(n)$。也就是说,为包含n个结点的单链表构建多级索引构成跳表,需要额外使用接近n个结点的存储空间。
如果每三个结点或这五个结点抽取一个结点构成上级索引,如下图所示:
空间复杂度的计算方式如下图所示:

和为$n/2$,空间复杂度同样是$O(n)$,但是相比于间隔为2,减少了一般的索引结点存储空间。
在实际工程中,单链表中的每一结点所存储的对象可能很大,此时,在构建索引结点时,只需要存储关键值和指针,不需要存储对象,因而当对象比索引结点大很多时,索引结点所占用的额外空间可以忽略不计。
高效的动态插入和删除
插入操作
跳表除了支持查找操作之外还支持动态的插入、删除操作,插入、删除操作的时间复杂度也是$O(logn)$。
在单链表中,如果要找到特定的位置并执行插入操作,查找操作比较耗时,而插入的时间复杂度为$O(1)$。而对于跳表来说,查找某个特定的插入位置的时间复杂度为$O(logn)$,找到插入位置后,插入操作的时间复杂度同样为$O(1)$。如下图所示:
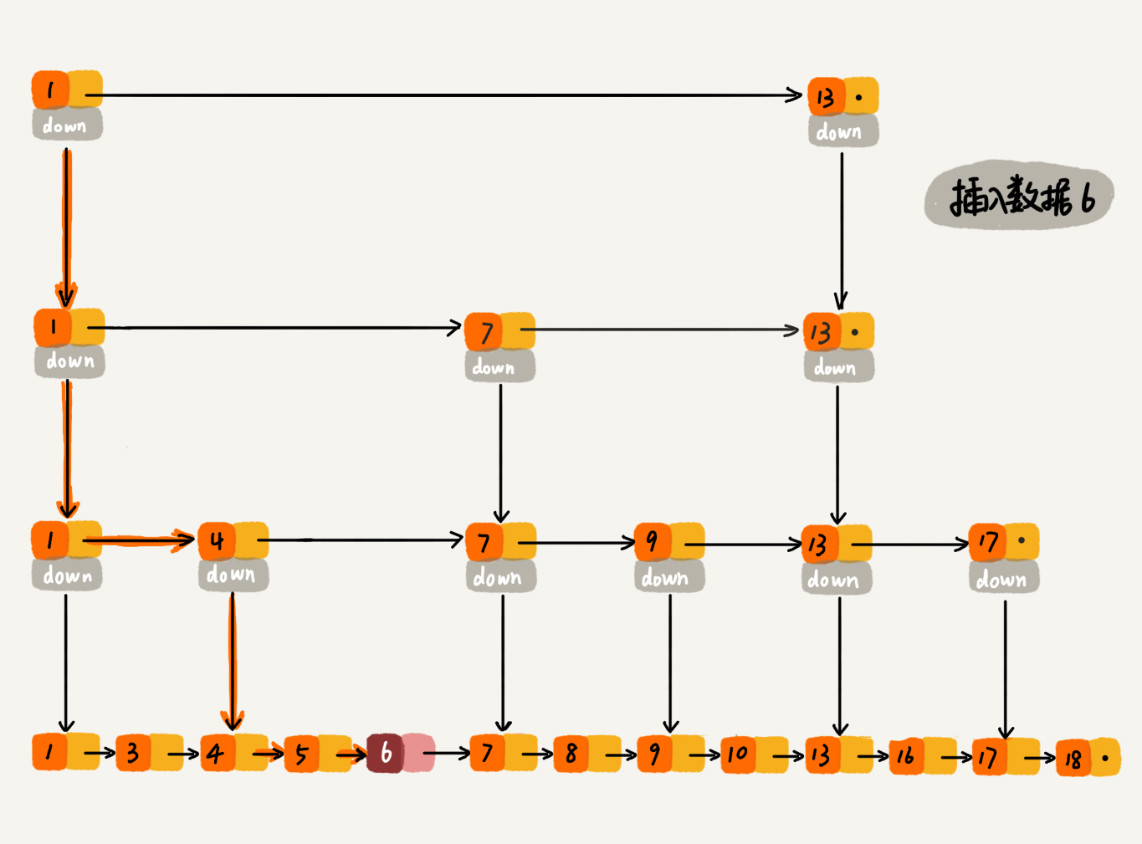
删除操作
在进行删除操作时,我们需要考虑的一点时,所删除的结点可能会在索引中出现,此时要同时删除索引中的对应结点。在进行删除操作时,要注意获取被删除结点的前驱结点。
跳表索引的动态更新
在往跳表中插入数据时,如果不进行索引的更新操作,会导致某两个索引结点之间的数据非常多,导致在对这一部分结点执行相关操作时效率底下。
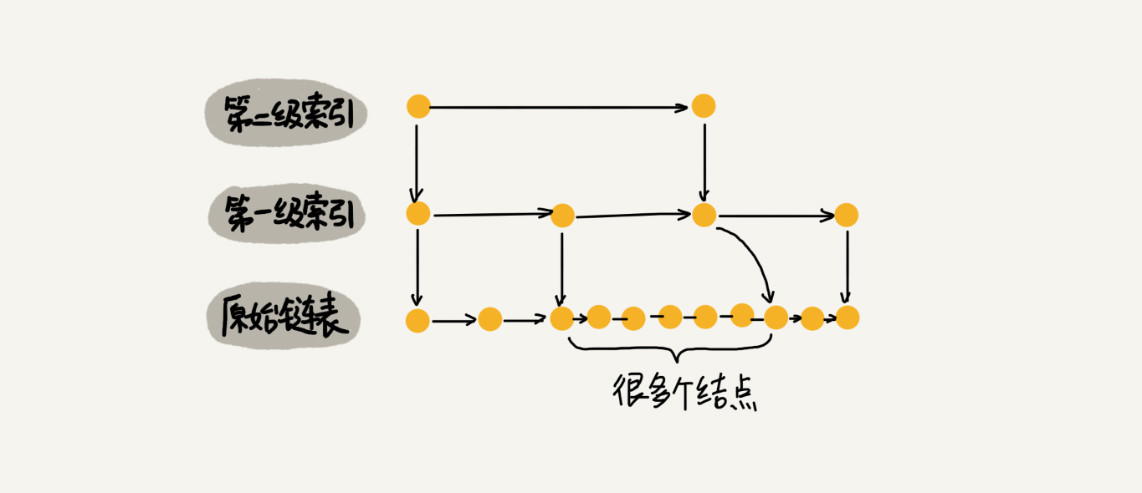
因而,我们需要一种手段来维护索引和原始链表大小之间的动态平衡。当链表中的数据增多时,就加入更多的索引结点。
当我们向跳表中插入数据时,可以选择同时将这个数据插入到部分索引层中。通过使用一个随机函数来决定将这个结点插入到哪几级索引中,例如随机函数生成的值为k,那么就将这个结点添加到第一级到第k级这k级索引中。
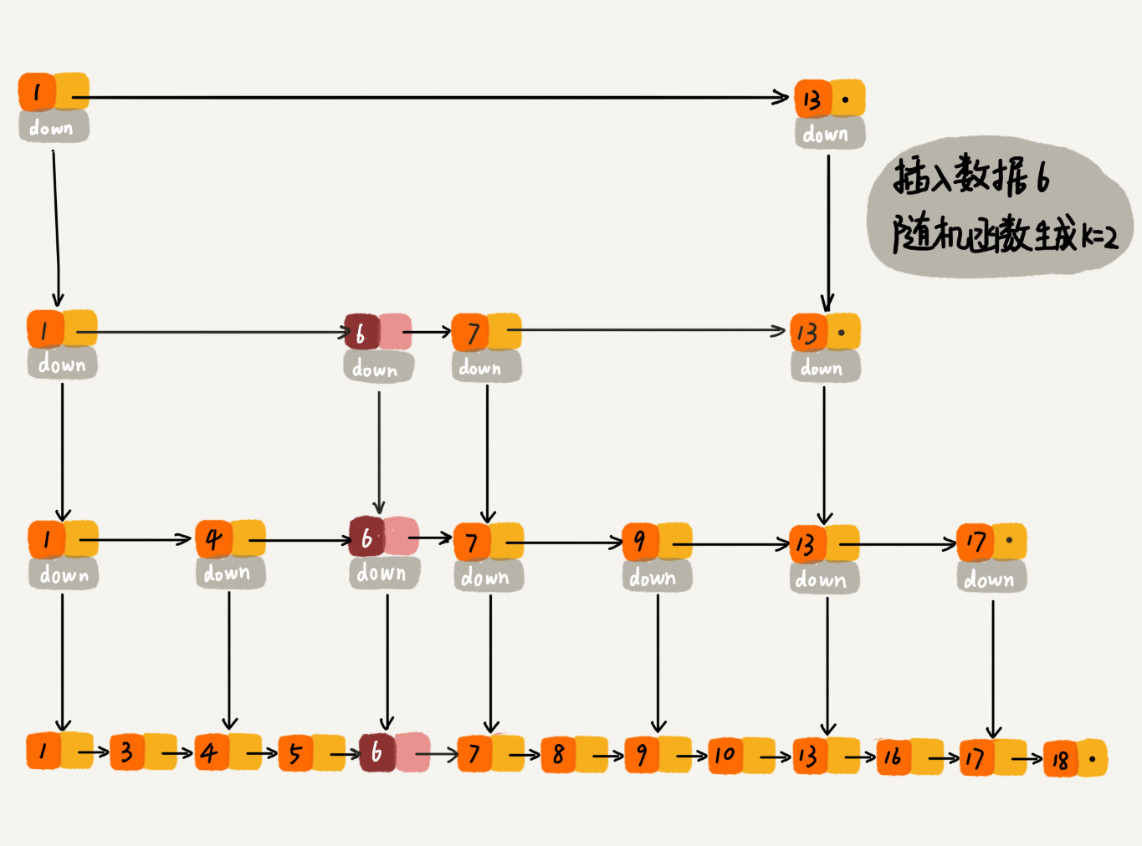
这里要注意的一点是,随机函数应该能够在概率上保证跳表的索引大小和数据大小相平衡。
在Redis中就使用跳表来实现有序集合,那么为何不使用红黑树呢?
Redis中的有序集合所支持的核心操作主要有以下几个:
- 插入一个数据;
- 删除一个数据;
- 查找一个数据;
- 按照区间查找数据([100, 356]之间的数据);
- 迭代输出有序序列。
其中的插入、删除、查找和迭代输出有序序列的操作使用红黑树也可以完成,时间复杂度和跳表一样。但是,按照区间查找数据的操作红黑树没有跳表效率高。
除此之外,还有跳表代码实现简单、更加灵活的特点。