使用链表实现LRU缓存淘汰算法

本文为数据结构与算法之美-王争的学习笔记，如需查看完整内容，请参考链接。

所谓缓存，是一种提高数据读取性能的技术，在硬件设计、软件开发中有着非常广泛的应用，如CPU缓存、数据库缓存和浏览器缓存等。

当缓存被用满时，就需要对数据进行清理。这时常用的清理策略有以下三种：先进先出策略FIFO（First In, First Out）、最少使用策略LFU（Least Frequently Used）、最近最少使用策略LRU（Least Recently Used）。

那么如何使用链表来实现最近最少使用策略呢？

什么是链表

链表和数组一样，是最基础的链表结构。两者的逻辑结构都是一种线性表，但两者在存储结构上存在很大的差别。我们已知在对数组进行存储时需要开辟一连串的连续内存，并向这一串内存中放入相同类型的数据。如果我们需要申请的连续的内存空间大于内存中最大的连续空间的大小，这时即时内存中总的剩余空间足够多，也会导致申请失败。如下图左侧所示（示意图来自数据结构与算法之美）。

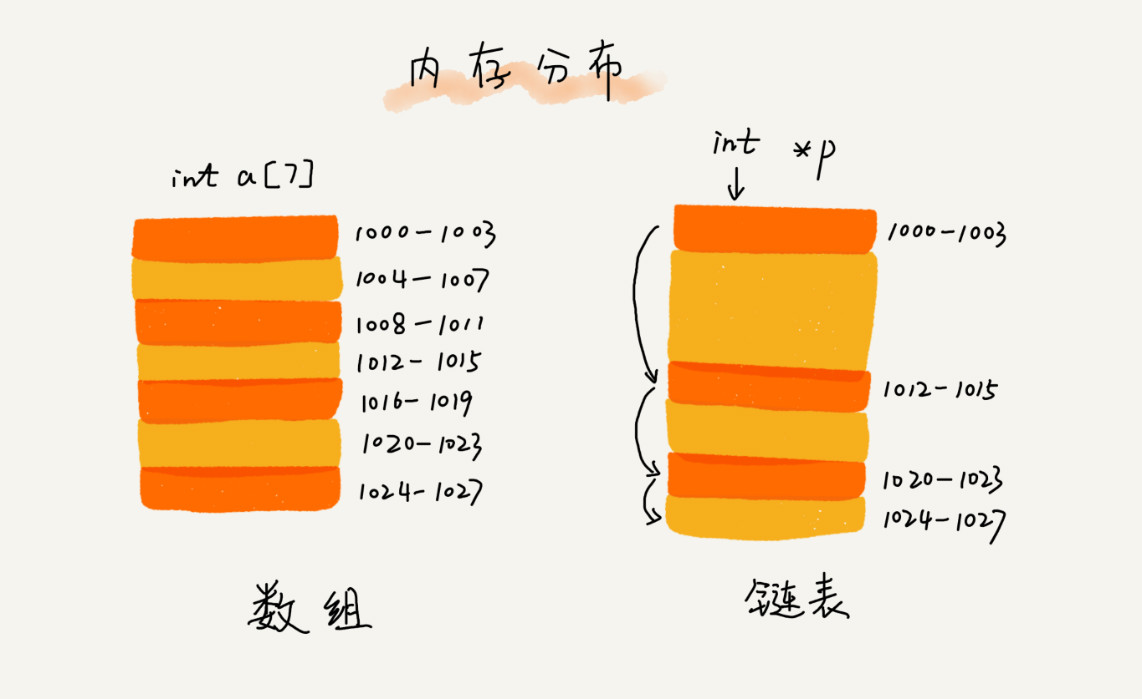
但如果使用的是链表便可以解决这一问题。与数组不同，链表使用的是内存中零散分布的一系列内存空间，这些内存空间之间使用“指针”连接，如上图右侧所示。

常用的链表有单链表、双向链表和循环链表三种。

单链表

在上面的描述中，我们了解到链表之间是通过指针进行连接的。那么在存储链表的过程中就需要对指针信息进行存储。在数组中，每一个位置存储的数据元素本身，而在链表中将每一个内存块称为结点。结点中除了要存储数据本身之外，还要存储链表的下一个结点的地址。将存储下个结点地址的指针称作后继指针（Next），将只有后继指针的链表称作单链表，如下图所示。

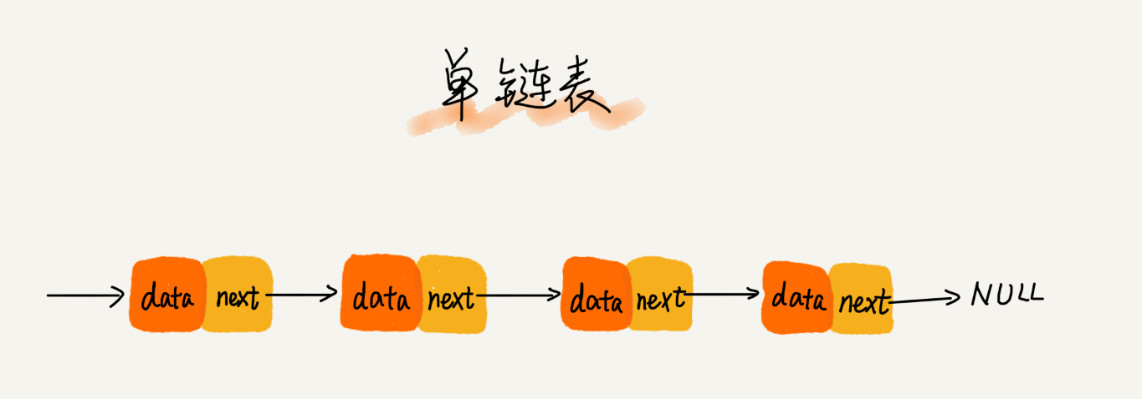
与数组一样，链表同样存在查找、插入和删除操作。在数组中，由于存储空间连续，依据查找的元素的下表和偏移地址计算公式可以很方便地计算出要查找的元素的位置，算法的时间复杂度为$O(1)$；但由于元素是连续存储的，插入和删除任何一个元素都需要对后续的所有元素进行移动，时间复杂度为$O(n)$。

针对这些问题，我们可以探究一下链表的查找、插入和删除操作。首先来看插入和删除操作，对于链表中的任何一个元素，在对其进行插入和删除操作时，我们并不需要移动其后的所有元素，因为我们不需要保证链表的存储空间为连续。任何时候进行插入和删除操作都只需要考虑相邻结点的操作，因而时间复杂度为$O(n)$，如下图所示。

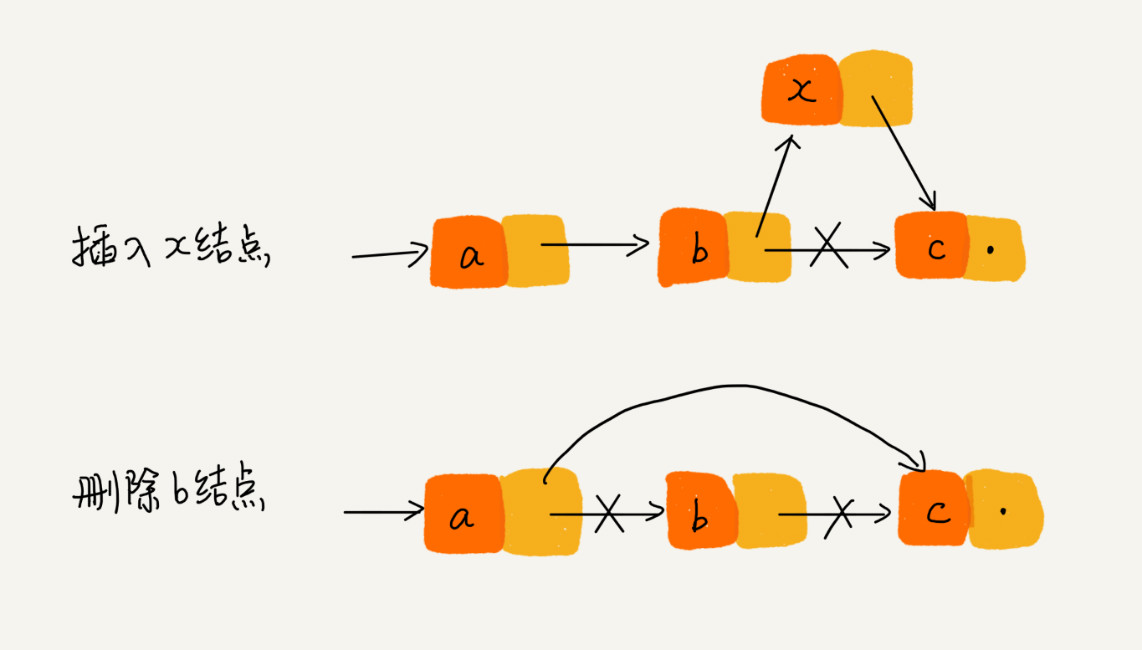
随机存储的特性降低了链表在插入和删除操作上的时间复杂度，但同时也给随机查找造成了一定的麻烦。在链表中，为了查找某一个位置的元素，只能从第一个位置开始向后遍历，直到找到对应的元素，时间复杂度为$O(n)$。

循环链表

循环链表是一种特殊的单链表，与单链表的区别在于尾结点。单链表的尾结点指向空地址，而循环链表的尾结点指向链表的头结点，呈现出一种首位相接的结构，如下图所示。

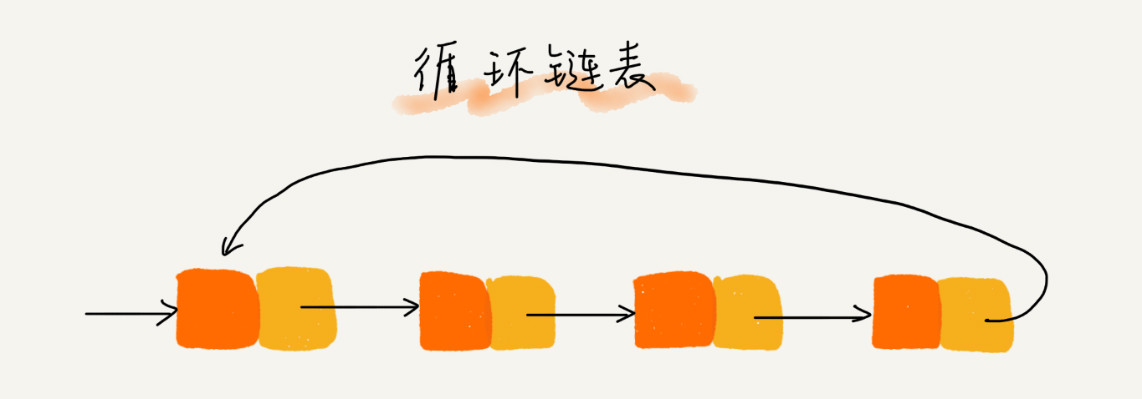
循环链表的特点是从链尾到链头的访问非常方便，当要处理的数据具有环形结构特点时，就适合采用循环链表。

双向链表

在单链表中只有一个后继指针（next）指向后继结点，而在双向链表中，除了后继指针外还存在一个前驱指针指向（prev）指向前驱结点。

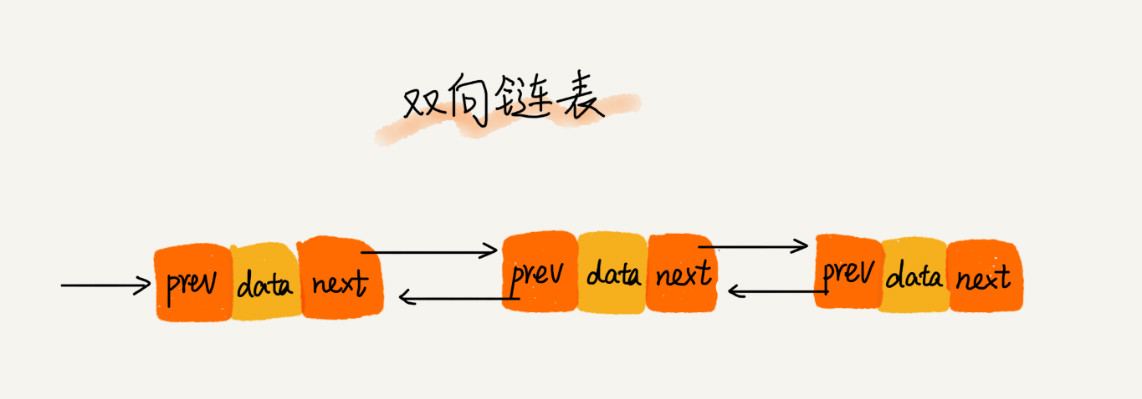
在存储空间方面，因为双向链表的每一个结点都需要额外存储一个前驱指针，所以相较于单链表，双向链表会占据更过的内存空间。但正是由于有个双向指针，双向链表在解决双向遍历问题时具有明显的优势。

那么相较于单链表，双向链表更适合解决那些问题呢？

双向链表支持$O(1)$时间复杂度内找到前驱结点，因而在某些情况下，双向链表的插入和删除操作比单链表更为高效。

删除操作

删除操作有两种情况：1）删除结点中等于某个给定值的结点；2）删除给定指针指向的结点。

对于第一种情况，单链表和双向链表所需的时间复杂度相同，都需要从第一个结点查找对应的结点，然后删除该结点。操作主要几种在查找对应元素上，时间复杂度为$O(n)$；对于第二种情况，我们需要找到该指针所指结点的前驱结点，单链表同样需要从第一个结点开始向后遍历。而对于双向链表来说，只需要使用前驱指针即可，时间复杂度为$O(1)$。
插入操作

与删除操作相同，当我们需要在指定结点的位置前插入一个结点时，双向链表的时间复杂度为$O(1)$，而单链表的时间复杂度为$O(n)$。

这实际上是一种利用空间换取时间的思想。对于执行较慢的程序，可以消耗更多的内存来进行优化，而对于消耗过多内存的程序，可以通过消耗更多的时间进行优化。

将双向链表和循环链表进行结合便可以得到双向循环链表，如下图所示：

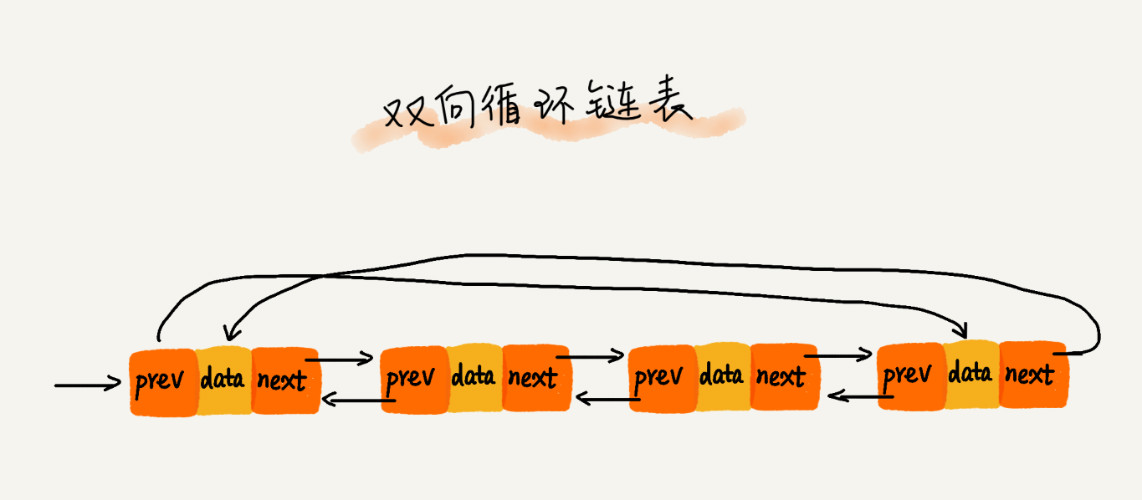
链表和数组的性能对比如图所示：

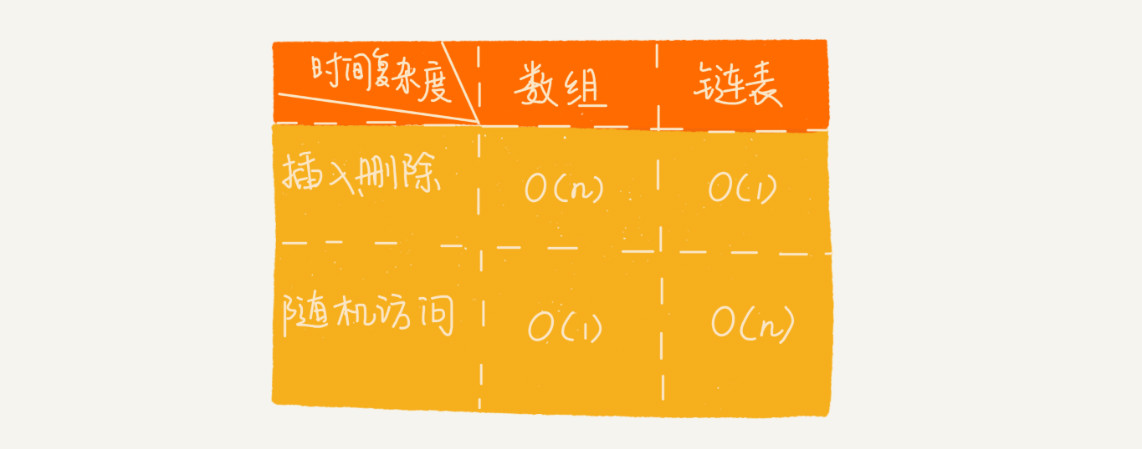
LRU缓存淘汰算法

LRU算法的全称是最近最少使用策略，意思就是以当前时间为基准，越少被使用的元素将越有可能被删除。可以使用有序单链表来实现，将越少被使用的元素放在链表的尾部，越多被使用的元素放在链表的头部，当缓存不足时直接从尾部删除元素即可，具体步骤如下。

如果当前数据已经在链表中，遍历得到该数据对应的结点，将其从原始位置删除并移至链表的头部。
如果当前数据不在链表中：
- 缓存未满，将该数据插入链表的头部。
- 缓存已满，删除链表尾部的元素，再将数据插入链表的头部。

该算法的时间复杂度未$O(n)$，因为无论何种情况下都要在单链表中进行查找操作，相比之下，插入和删除操作只消耗很少的时间。

如何编写链表代码

使用哨兵简化实现难度

以单链表的插入为例，如下图所示：

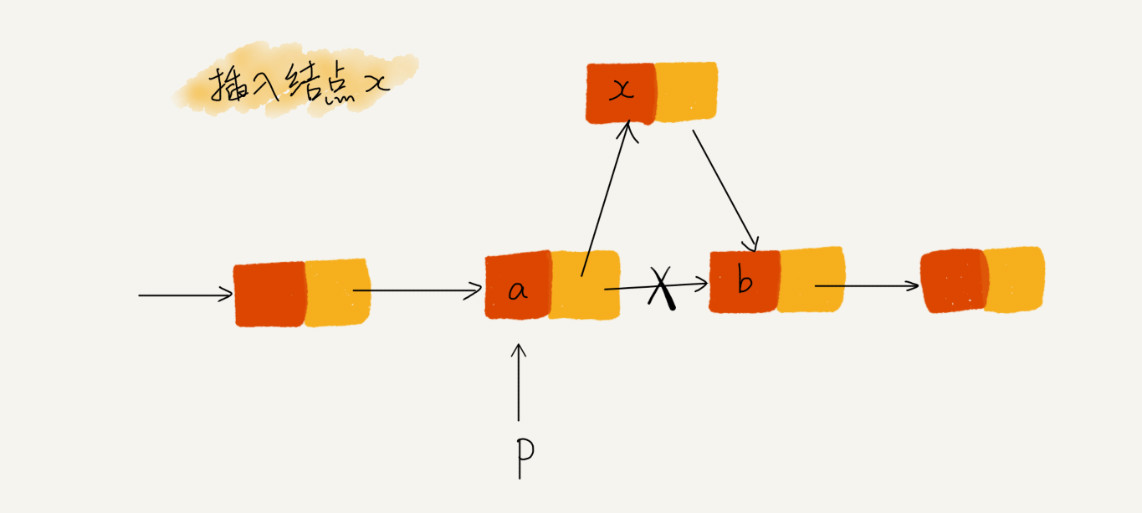
如果要在结点p后面插入一个新的结点，只需要如下两行代码即可：

1 2	new_node->next = p->next; p->next = new_node;

但如果要向一个空链表插入第一个结点时，就无法使用这一代码，因为此时链表的表头指向为空。因而应该使用如下的逻辑：

1
2
3

if (head == null) {
  head = new_node;
}

同理对于单链表中的一般结点的删除操作，只需要一行代码即可：

1	p->next = p->next->next;

但是，如果删除的结点为单链表的最后一个，就需要使用如下代码：

1
2
3

if (head->next == null) {
   head = null;
}

也就是说，我们需要在插入和删除单链表的结点时，分别对第一个和最后一个结点进行特殊处理。为了解决代码编写时的麻烦，我们可以引入哨兵元素，所谓哨兵即为了防止操作越界。在单链表中，我们可以声明一个哨兵结点，单链表的head指针会一直指向该哨兵结点，将这种链表称为带头链表，如下图所示。

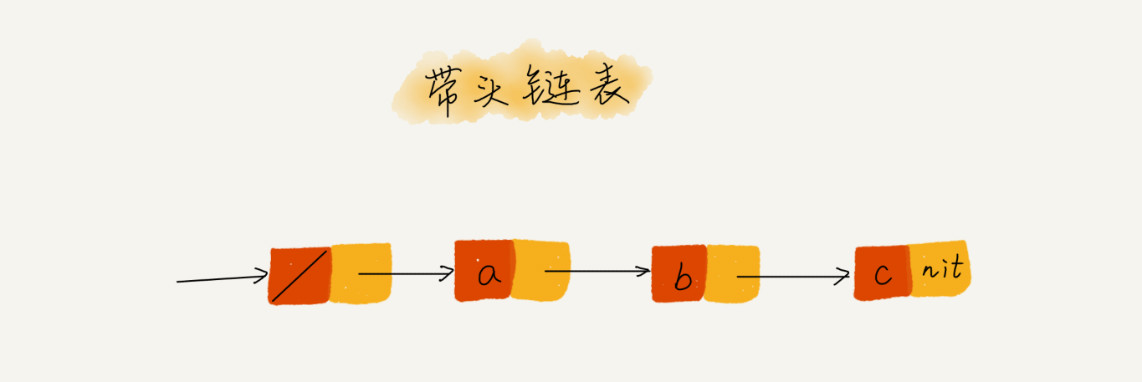
通过加入哨兵结点，便可以将链表的插入和删除操作统一起来。

重点留意边界条件的处理

在进行软件开发中，需要特别留意代码运行时的一些边界条件是否满足。代码不仅要在一般情况下能够正常运行，还需要能够对一些异常情况进行处理。编写链表代码时常用的边界条件有以下几点：

链表为空时是否工作正常。
链表中只有一个元素时是否工作正常。
链表中有两个元素时是否工作正常。
代码在处理头结点和尾结点时是否工作正常。

善于使用举例法和画图法

有些情况下，只依靠抽象的思考是无法理清代码逻辑的，这时候就需要使用举例法和画图法。比如上述所说的插入操作的三种不同情况：1）链表为空时插入；2）在表头插入；3）在两个元素之间插入。可以画图如下：

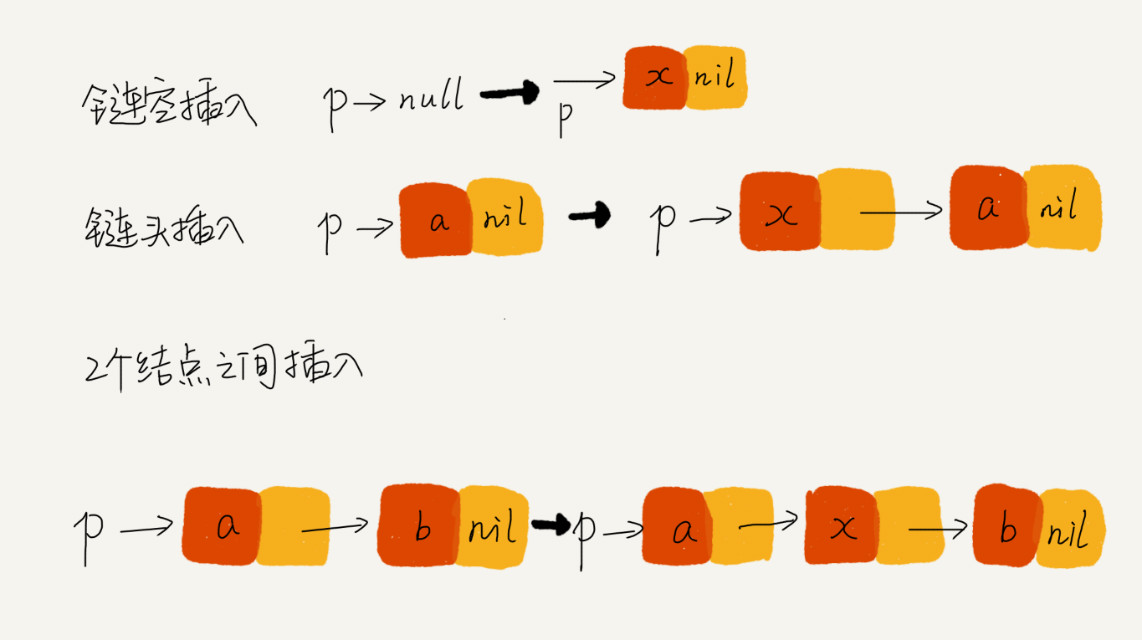
多写多实践

无论如何，代码只有多写才能发现问题。正所谓孰能生巧。

参考

数据结构与算法之美-王争