散列表-中

我们知道当散列函数设计不恰当时，很容易造成散列冲突，有些恶意的攻击者会利用这一点通过精心构造数据，使得所有的数据经过散列函数后都被散列到同一个槽中。当使用的是基于链表的冲突解决方法时，散列表就会退化为链表，查询的时间复杂度就从$O(1)$退化为$O(n)$。这就时散列碰撞攻击的基本原理。

那么如何设计一个可以应对各种异常情况的工业级散列表，避免在散列冲突的情况下，散列表的性能急剧下降，同时达到抵抗散列碰撞攻击的目的？

设计散列函数

在设计散列函数时，有以下几点要求：

散列函数的设计不能太复杂：过于复杂的散列函数会消耗大量的计算资源和时间，间接地也会影响散列表的性能。
散列函数生成的值要尽可能随机且均匀地分布，这样才能避免或者最小化散列冲突，即使出现散列冲突，由于散列到各个槽中的数据比较平均，也可以避免某个槽内数据特别多的情况。

装载因子

当装载因子过大时，说明散列表中有过多的元素，空闲位置很少，散列冲突的概率就会很大。

对于没有频繁插入和删除的静态数据集合，我们可以根据数据的特点、分布等，设计出完美的、有极少冲突的散列函数。而对于动态散列表，数据集合频繁变动，随着数据的加入，装载因子就会变大，装载因子太大时散列冲突就会变得很严重。

此时，可以使用动态扩容的思想，重新申请一个更大的散列表，将数据搬移到新的散列表中，这样装载因子就会变小。

如果是对数组进行扩容，在进行数据搬移时会非常简单，但是如果对散列表进行动态扩容，因为散列表的大小发生了变化，在进行数据搬移时就需要重新计算数据的存储位置。如下图所示：

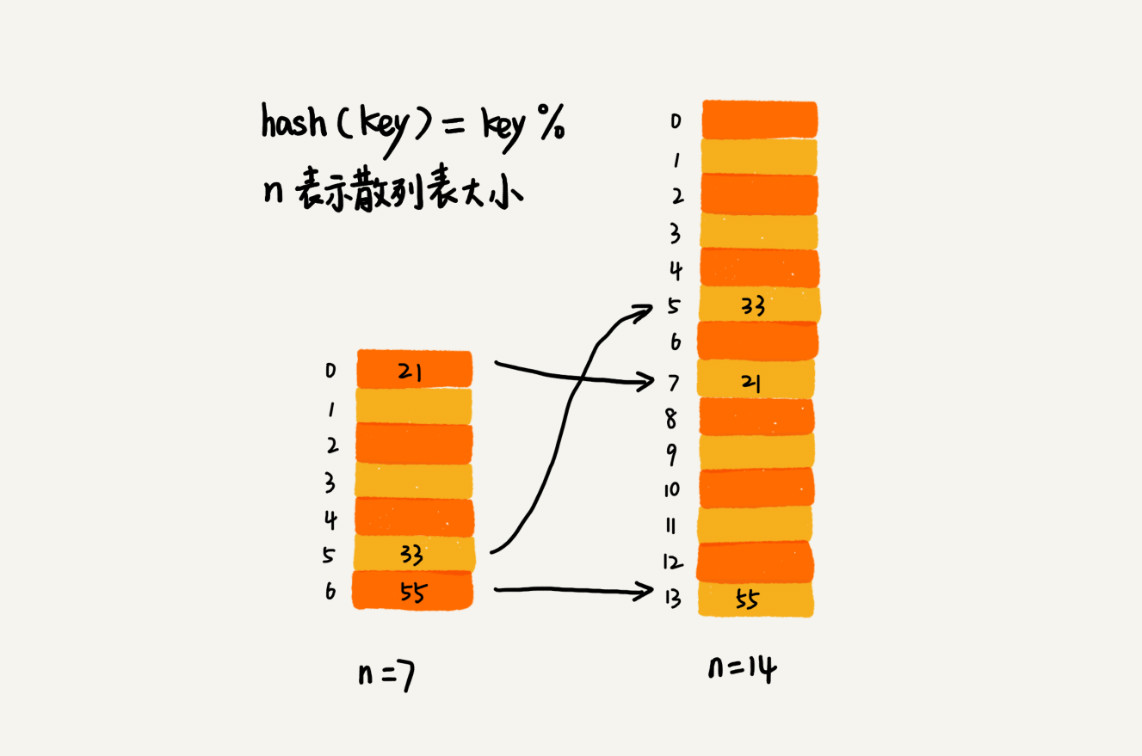
对于支持动态扩容的散列表，在进行插入操作时，使用摊还分析法可以知道时间复杂度为$O(1)$。

如何避免低效扩容？

在进行动态扩容操作时，可能会非常低效，例如散列表的大小为1GB，要进行动态扩容就需要对1GB的数据重新计算哈希值，并进行数据搬移，此时便会非常消耗时间。

上述的一次性扩容的操作是难以接受的，为此，我们可以将扩容操作穿插在插入操作过程中，分批完成。当装载因子触达阈值之后，只申请新空间而不进行数据搬移操作。

在达到装载因子阈值后，执行插入操作时，将新数据插入到新的散列表中，同时从旧的散列表中拿出一个数据放入新散列表中；每次插入一个新数据，就执行上述过程。这样，旧的散列表中的数据就被分批搬移到新的散列表中，从而避免了集中的数据搬移。

当进行查找操作时，首先在新散列表中查找，再在旧的散列表中查找。这样，就将一次集中扩容的时间均摊到多次插入操作中，这种方式下，任何时候进行插入操作的时间复杂度都是$O(1)$。

如何选择冲突解决方法？

在解决散列冲突时主要有两种方法：开放寻址法和链表法。那么两者的优缺点各是什么？

开放寻址法

开放寻址法的数据都存储在数组中，因而可以有效利用CPU缓存加快查询速度。并且相对于链表法，在进行序列化时更加容易。

但是开放寻执法在删除数据时比较麻烦，并且更容易发生散列冲突，装载因子的上限不能太高。因而，开放寻址法适用于数据量较少且装载因子小的情况。

链表法

链表法具有更高的内存利用率，且对大装载因子的容忍度更高。但是，链表需要额外存储指针，因而对于比较小的对象的存储，比较消耗内存，并且链表中的结点的存储不是连续的，因而对CPU缓存不友好，对执行效率也有一定的影响。

但如果存储的是大对象，那么指针的消耗就可以被忽略。实际上，我们可以对链表法中的链表进行改造，将其替换为其他高效的动态数据结构，如跳表、红黑树等，这样即使出现散列冲突，所有的数据都被散列到一个桶内，查找时间复杂度也是$O(logn)$，可以有效避免散列碰撞攻击。

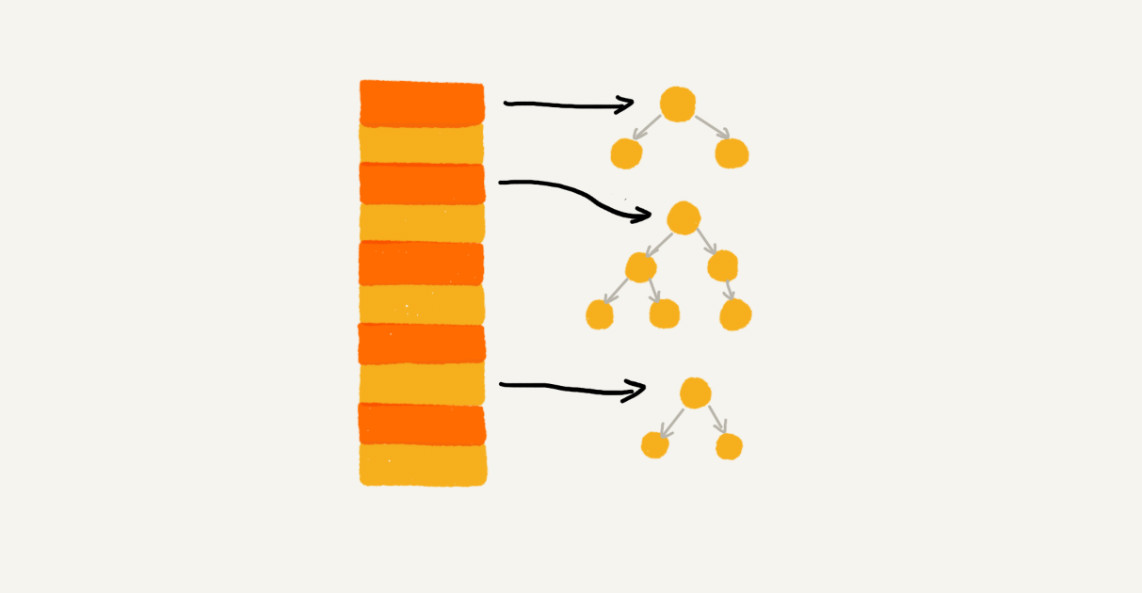
因而，基于链表的散列冲突解决方法更适合存储大对象、大数据量的散列表，并且相比于开放寻址法更为灵活，支持更多的优化策略。

工业级散列表

以Java中的HashMap为例：

1. 初始大小

HashMap的默认初始大小为16，也可以手动设置这一值以减少动态扩容的次数。

2. 装载因子和动态扩容

最大装载因子默认为0.75，当HashMap中元素个数超过0.75*capacity时，则进行动态扩容，每次扩容会扩大为原来的两倍大小。

3. 散列冲突解决方法

HashMap底层采用链表法解决冲突。当链表的长度过长时，就将链表转换为红黑树；而当红黑树的个数小于8时，又会将红黑树转换为链表。

4. 散列函数

散列函数的设计追求简单高效、分布均匀。

int hash(Object key) {
    int h = key.hashCode()；
    return (h ^ (h >>> 16)) & (capitity -1); //capicity表示散列表的大小
}

其中，hashcode()返回的是Java对象的hash code。例如，String类型的对象的hashCode()如下所示：

public int hashCode() {
  int var1 = this.hash;
  if(var1 == 0 && this.value.length > 0) {
    char[] var2 = this.value;
    for(int var3 = 0; var3 < this.value.length; ++var3) {
      var1 = 31 * var1 + var2[var3];
    }
    this.hash = var1;
  }
  return var1;
}

如何设计工业级的散列表

何为工业级的散列表？工业级的散列表应该具有那些特性？

支持快速的查询、插入和删除操作；
内存占用合理，不浪费过多的内存空间；
性能稳定，极端情况下也不会退化到难以接受的地步。

那么如何实现这一目标？可以有以下几点考虑方向：

设计合理的散列函数；
定义装载因子阈值，引入动态扩容策略；
选择合适的散列冲突解决方法。

参考

数据结构与算法之美-王争