行人重识别入门
什么是行人重识别?
行人重识别的定义
行人重识别,也称行人再识别(ReID),其任务是希望能够利用计算机视觉的算法来进行跨摄像头的追踪,也就是找到不同摄像头下的同一个人,这也是图像检索的一个子问题,同时因为摄像头的距离比较远,所以人的图像都比较模糊,没有办法通过人脸来定位,同时 ReID 更希望解决跨摄像头的问题,所以周围的环境以及摄像头的变化都会增加 ReID 的难度(sherlock)。

如上图所示(出处见图片水印),左侧一列图片为query集,右侧的所有图片为gallery,我们的任务就是从右侧的gallery集中找出和query为同一人的图片。
行人重识别的评价指标
行人重识别常用的评价指标主要有两种:
rank1
即首位命中率,对于query中的一张图片会和gallery中的每一张图片都计算一个距离,然后将距离进行排序,判断排序后的第一张的ID是否和query相同;而rank5表示排序后的前五张中是否有一张命中。
mAP
mAP表示平均精度,如下图所示:
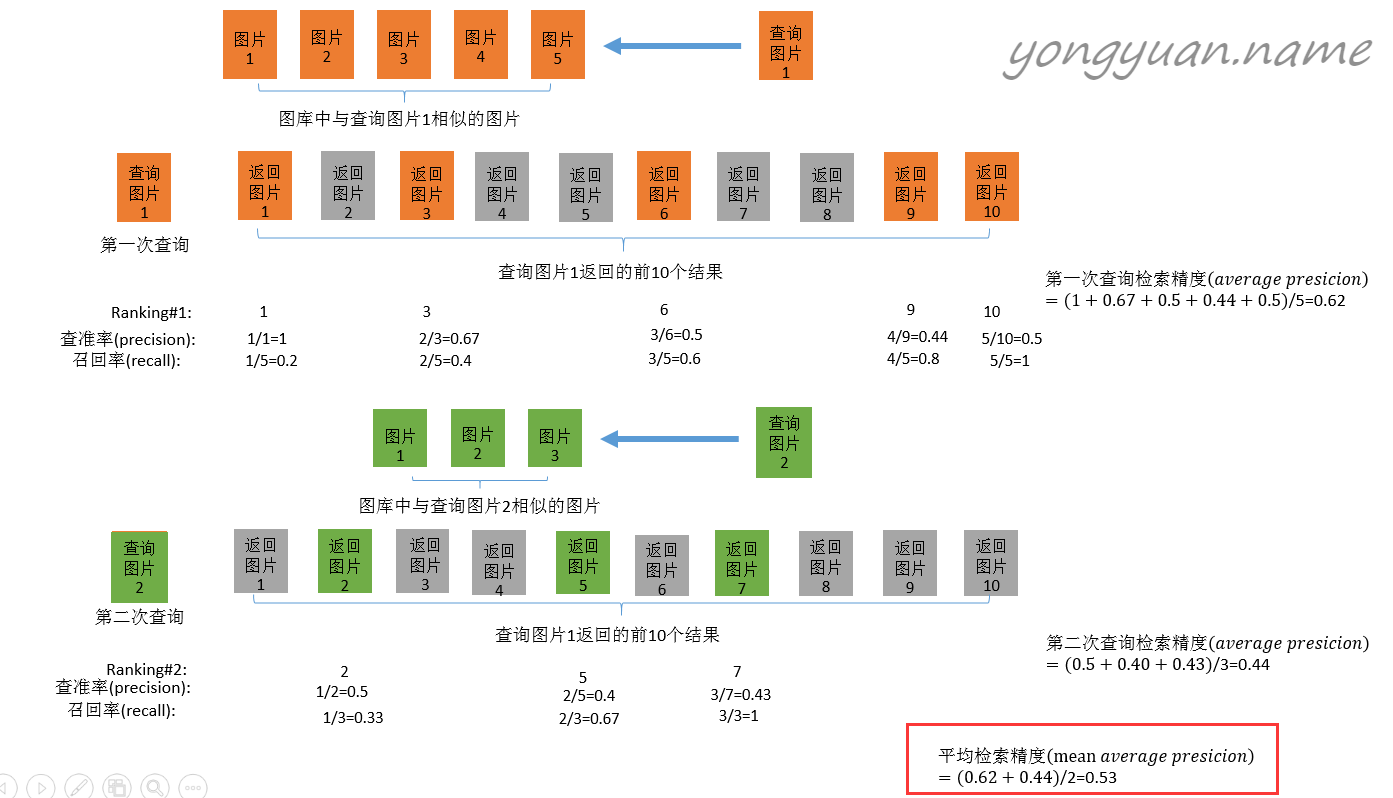
对于一张query图片,从gallery中得到前10个结果,对于不同的rank,其中正确识别的图片占总的返回的10个图片的比例被称为各个rank的查准率,正确识别的图片占该ID所有图片的比例被称为查全率;取不同rank的查准率的平均值便得到AP(average precision);对query中所有的图片的AP取平均值便可以得到整个query的mAP。上图来自:图像检索:信息检索评价指标。
常见的行人重识别方法
行人重识别方法可以被划分为以下几类:
- 基于表征学习的ReID方法
- 基于度量学习的ReID方法
- 基于局部特征的ReID方法
- 基于视频序列的ReID方法
- 基于GAN造图的ReID方法
基于表征学习的ReID方法
基于度量学习的ReID方法
度量学习被广泛应用于图像检索领域,不同于表征学习给出行人的类标,度量学习旨在通过网络学习出两张图片的相似度。通过对损失函数进行设计,使得相同行人的图片(正样本对)的距离尽可能小,不同行人图片(负样本对)的距离尽可能大。常用的度量学习算是方法有:
- 对比损失(Contrastive loss)
- 三元组损失(Triplet loss)
- 四元组损失(Quadruplet loss)
- 难样本采样三元组损失(Triplet hard loss with batch hard mining, TriHard loss)
- 边界挖掘损失(Margin sample mining loss, MSML)
假设有两张图片,经过网络的前向传播后得到其归一化后的向量$f_{I_1}$和$f_{I_2}$,定义两个特征向量之间的欧氏距离为:
对比损失
有如下孪生网络结构,输入一对图片$I_a$和$I_b$,两者可为同一或不同行人的图片,当两者为同一行人的图片时,此对图片的标签为$y=1$,否则为$y=0$。
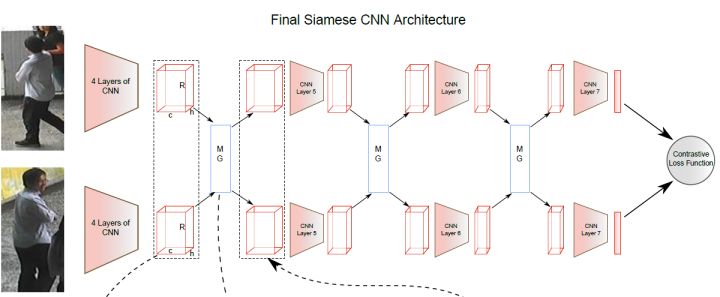
定义对比损失如下:
其中$(z)_+$表示$max(z,0)$,$\alpha$为可调整的阈值参数。在训练过程中,为了最小化损失函数,对于正样本对,$d_{I_a,I_b}$会逐渐变小,相同ID的行人图片会逐渐在特征空间中形成聚类;对于负样本对,$d_{I_a,I_b}$会逐渐变大,直到超过设定的阈值时,认为负样本对被完全区分开,此时该负样本对的损失为0。
最终,正样本对的距离逐渐变小,负样本对的距离逐渐变大。从而,在预测时,输入一对图片便可以判定是否属于同一个行人。
三元组损失(Triplet loss)
三元组损失是一种被广泛应用的度量学习损失。三元组损失需要三张输入图片,包含一对正样本和一对负样本。三张图片分别对应固定图片(Anchor)$a$,正样本图片(Positive)和负样本图片(Negative)$n$。固定图片和正样本图片为正样本对,固定图片和负样本图片为负样本对。三元组损失表示为:
三元组损失的作用如下图所示:拉近正样本对之间的距离,增大负样本对之间的距离,使得相同ID的行人图片在特征空间中形成聚类。
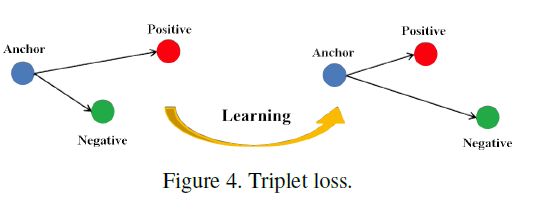
改进三元组损失:有论文认为三元组损失只考虑了正负样本对之间的相对距离,而没有考虑正样本对之间的绝对距离,提出改进的三元组损失:
四元组损失
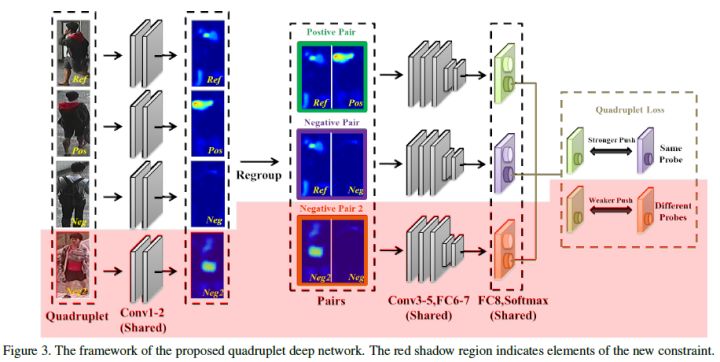
与三元组损失相比,四元组损失需要四张输入图片,四张图片分别为固定图片(Anchor)$a$,正样本图片(Positive)$p$,负样本图片1(Negative1)$n_1$和负样本图片2(Negative2)$n_2$。其中$n_1$和$n_2$是两张不同行人ID的图片,四元组损失表示为:
其中$\beta$常小于$\alpha$,前一项称为强推动,后一项称为弱推动。
相比于三元组损失只考虑正负样本间的相对距离,四元组添加的第二项不共享ID,因而考虑的是正负样本间的相对距离。
难样本采样三元组损失(Triplet loss with batch hard mining, TriHard loss)
传统的三元组损失随机从训练数据中抽取三张图片,做法简单但是抽样出的大部分都是简单易区分的样本对。样本对简单是不利于网络学习到更好的特征的。研究表明用更难的样本去训练网络能够提高网络的泛化能力。
TriHard损失的核心思想是:对于一个训练batch,随机挑选$P$个ID的行人,每个行人随机挑选$K$张不同的照片,那么一个batch含有$P\times K$张图片。对于batch中的每一张图片$a$,从剩余样本中挑选一个最难的正样本和一个最难的负样本组成一个三元组。
定义和$a$为相同ID的图片集为$A$,剩下不同ID的图片集为$B$,TriHard损失表示为:
其中$\alpha$为人为设定的阈值。TriHard损失会挑选与$a$距离最远的正样本和距离最近的负样本来构成三元组。一般情况下,TriHard损失的效果由于传统三元组损失。
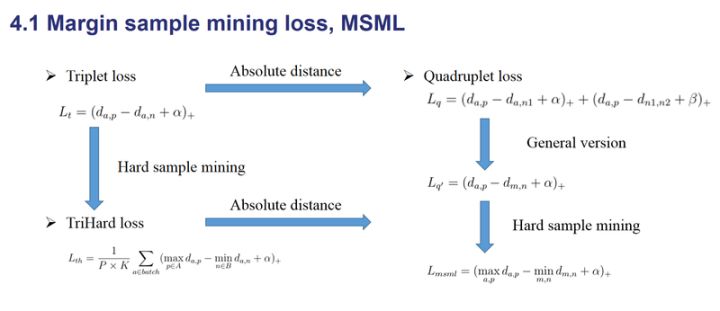
边界挖掘损失(Margin sample mining loss, MSML)
TriHard损失对一个batch中的每一张图片都挑选出最难的正样本和最难的负样本构成三元组计算损失,而MSML只挑选出一个batch中最难的一对正样本对和最难的一对负样本对计算损失,可以将MSML看做更难的一种难样本采样,形式如下:
其中,a和m可以是正样本对也可以是负样本对,因而同时兼顾了正负样本对的相对距离和绝对距离。$max_{a,p}d_{a,p}$可以看做正样本对的上界,$min_{m,n}d_{m,n}$可以看做负样本对的下界,MSML使得正负样本对的边界的间距变大。因而被成为边界样本挖掘损失。
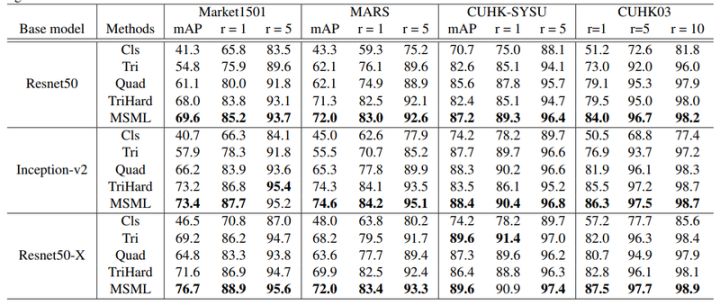
损失函数性能的对比
基于局部特征的ReID方法
上面的方法都是将一整幅图送入神经网络得到单个特征向量,属于一种全局特征,后面,研究者又提出了使用局部特征的方法。
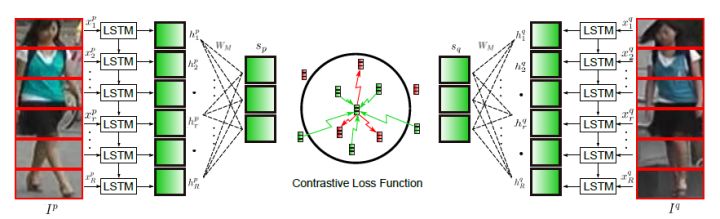
图像切块
将行人图片进行垂直切割,按顺序送入长短时记忆网络中,最后的特征融合了所有图像块的局部特征,但是缺点在于对图像对齐的要求比较高。
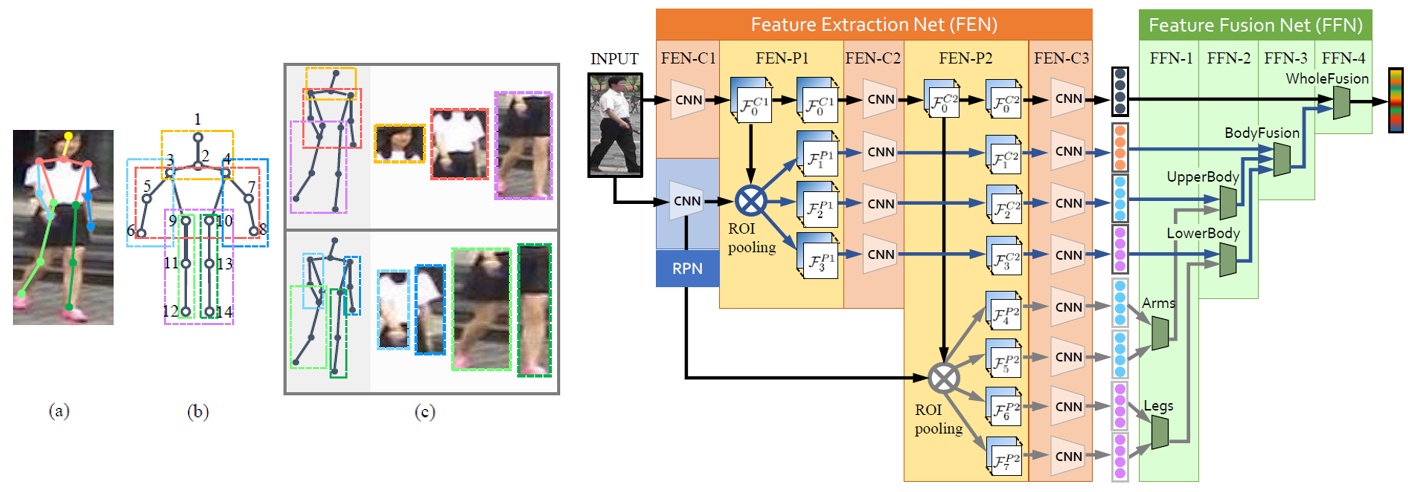
为了解决图片不对齐的问题,研究者借助人体姿态和关键点等信息对图像进行仿射变换,以是的图像对齐。也有一种方法时,在进行关键点检测后不使用仿射变换,而是依据关键点提取多个人体结构的感兴趣区域。
除了上述两种行人重识别方法之外还有基于视频的行人重识别方法和基于GAN生成的行人重识别方法,这两个方法都是为了得到更多的信息。
如何训练和测试行人重识别模型?
训练
ReID的basemodel主要使用一个backbone网络,如ResNet等,使用预训练权重进行初始化;损失函数主要使用分类的交叉熵损失或者度量学习的三元组损失。
测试
去掉backbone后面的全连接层,使用网络提取特征,计算查询集(query)和图片集(gallery)所有图片的特征之间的距离,根据距离计算rank1和mAP得到最后的结果。
行人重识别常用Tricks
Baseline Model
在论文中一般使用ResNet50作为基础模型(可以将最后一个卷积块的步长修改为1,得到的特征图增大一倍)。除此之外,可以使用三种损失函数:softmax、triplet hard和softmax+triplet。
加入BNNeck
常用的baseline中通常会同时使用分类损失和三元组损失,分类损失的作用是学习几个超平面将特征向量划分到不同的子空间中,对于分类损失而言,如果对特征向量进行了归一化,使其位于一个超球面上,此时分类损失的优化效果会更好;而三元组损失的作用是正样本对的特征向量在空间中离得更近,负样本对的特征空间在空间中离得更远,如果将特征向量限制在超球面上,三元组损失将正负样本推开的难度会增大。
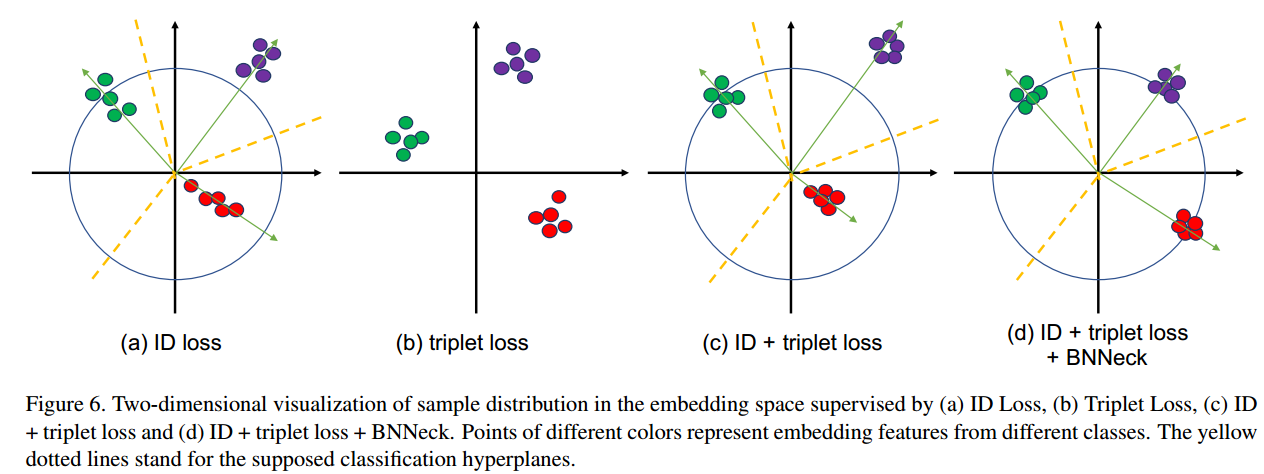
因而,如果分类损失和三元组损失使用的都是经过归一化的特征向量,往往会出现分类损失和三元组损失不同步收敛的情况。
为了解决这一问题,将网络经过全局池化得到的特征图(欧式空间)直接用于计算三元组损失,这一特征被称为$f_t$。接着将特征$f_t$经过一层BN层得到$f_i$,此时的特征图已经被近似归一化到超球面附近。
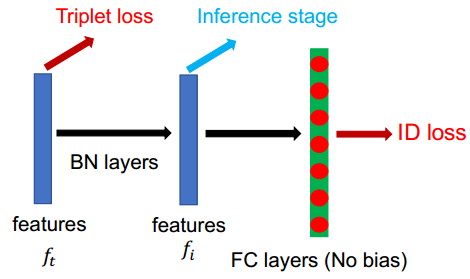
同时,用于分类的全连接层未使用偏置,因为Softmax函数是关于原点对称的,去掉偏置后,特征图会关于原点对称,进而保证分类的超平面一定经过原点。
中心损失(Center Loss)
三元组损失的缺点之一是只考虑了相对距离,损失大小与正样本对的绝对距离无关。假如三元组损失中的$\alpha$参数为0.3,正样本对的距离为1.0,负样本对的距离为1.1,此时损失为0.2;假设正样本对的距离为2.0,负样本对的距离为2.1,损失同样为0.2。为了加强正样本对之间的聚类性能,引入中心损失:
学习率唤醒策略(Warm-Up Strategy)
这是一种学习率调整策略,即在训练开始阶段先给学习率一个较小的初始值,接着慢慢增大,一段时间后又慢慢衰减。如下述公式所示:
学习率变化曲线:
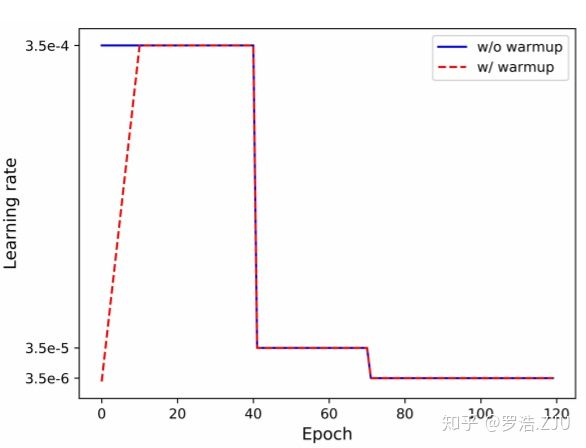
Loss
分别使用上述的三种损失函数,softmax损失使用图像分类的策略进行样本的选取;训练triplet hard和softmax+triplet hard在每个batch采样32个人,每个人采样4张图片。
输入大小和Batch Size
使用了不同的输入大小和batch size,最终的结果如下:
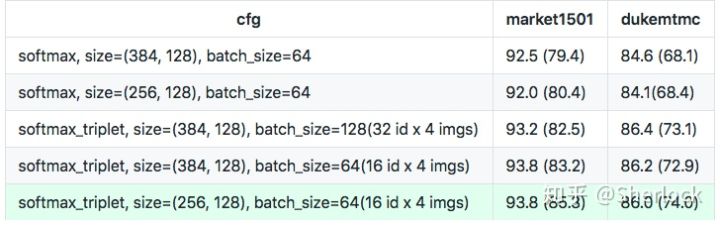
随机擦除数据增广
在图片中随机选取一块区域,加上噪声掩膜,这个掩膜可以是固定值(黑块、灰块)或者随机正太噪声。随机数据擦除属于数据增广的一种方式,可以降低模型过拟合的程度,进而提升模型的性能。

标签平滑(Label Smoothing)
标签平滑是一种应用于分类任务的策略。传统的分类任务使用交叉熵损失,标签使用one-hot编码,但one-hot编码是一种很强的监督约束,为了缓和标签对于网络的约束,可以对标签进行平滑:
例如,原始标签为$[0,0,1,0,0,0]$,设置平滑系数为0.1,那么平滑之后的标签为:$[0.02,0.02,0.9,0.02,0.02,0.02]$,同时损失应该由交叉熵变为相对熵,标签平滑可以降低模型的过拟合程度。